Numbers, Ratios, and Cycles

By: Joe Duffy

The following is an excerpt from Joe Duffy's Turning Point Analysis in Price and Time

Primary Numbers, Ratios, and Cycles

When first studying original W.D. Gann materials, one can be struck by the fact that Gann seemed to think that virtually every number and division was an “important” one. This characteristic allows one to see, in retrospect of course, that one or more of the “important” numbers played a part in turning the market at a particular point in price and time. If one stops their investigation of Gann, one could easily assume that Gann considered so many numbers significant, as to be practically useless as market forecasting tools.

While it is true that Gann did in fact write that many numbers and divisions were important, a practical and objective study leads one to conclude that most of Gann’s more public writing was perhaps a diversion. What Gann discovered that really works, he reveals more in theory than in specifics.

By theory, I mean that the essence of all Gann’s work is based on simple geometric relationships. The geometric configurations used by Gann are the circle, the square, and the triangle. In three dimensional terms, these are the sphere, the cube, and the pyramid.

Gann was not the only historical figure of note to find power and substance in basic geometry. Leonardo Da Vinci consciously used these configurations, as well as the Fibonacci ratios, in much of his work. Isaac Newton had a Fibonacci circular spiral and triangle carved into the headboard of his bed. In a self portrait, Pythagoras held in his hand a pyramid, which he proclaimed contained the key to the universe. In the modern era, Albert Einstein accorded great respect to simple geometry, and to its repetitive nature and power as it played out throughout the Universe.

Therefore, by studying the numbers and ratios most associated with basic geometry, you can discover the basis for both Gann’s number cycles, as well as the Fibonacci numbers and ratios. These numbers are prevalent and repetitive in many areas of nature. By starting from this premise, I have found it possible to separate the truly significant from the marginally useful, in the application of number cycles and ratios in the financial markets.

Following is a brief discussion of important number cycles, as well as speculation as to their possible derivation.

The circle contains 360 degrees, which is very close to the number of days in the earth’s solar year. Our solar year is also divided into 90 degree segments according to solstice and equinox, based on the relative position of the earth as it revolves around the sun. Therefore, the numbers 360 and 90 represent two important number cycles which have a firm and repetitive foundation in geometry and nature.

The square also contains four angles of 90 degrees, for a total of 360 degrees, reaffirming the importance of 90 and 360 as natural number cycles.

The triangle is formed by dividing the square from corner to corner in a diagonal fashion. This creates two 45 degree angles, and one 90 degree angle, for a total of 180 degrees. Hence we will add 45 to 180 to our important natural number cycles.

All of the natural number cycles mentioned thus far, plus many more, are contained in what is perhaps the most magical formation of all, the pyramid. It was noted above that the mathematician Pythagoras believed that the pyramid contained the “key to the universe.” It is also generally conceded that Leonardo Fibonacci, the 13th century mathematician, discovered what are now known as the Fibonacci number series and the Fibonacci ratios, through this study of the Egyptian pyramids.

The Egyptian pyramids are, of course, the most well known pyramids of all and include the Great Pyramid of Gizeh. The latter contains many fascinating natural number ratios and cycles which are representative of many cycles in nature, including those applicable to the financial markets.

The total length of the pyramid is exactly 100 times the solar year calculated to the second decimal point. The pyramid is 5,813 inches high, and as you will recall 5-8-13 are all Fibonacci series numbers. The angle of the slope of the pyramid walls is 51.8 degrees. Note that this is exactly the Fib ratio of 38.2 degrees away from 90 degrees or vertical. The corners of each side also divide the square base at 45 degree angles. Additionally, the ratio of the edges to the height of the pyramid are in the exact .618 Fib ratio.

Hence, the Golden Section ratios and Fibonacci number series are very significant.

Secondary Numbers, Ratios, and Cycles

The above discussion highlights the derivation of the most important numbers for use in trading. These are the ones that I have found to be most important in my own trading experience. Gann in particular felt that other numbers were also significant. These other numbers find their basis in other areas besides geometry, including Gann’s study of numerology, astronomy, astrology, and biblical references. A quick review of some of these follows:

The number cycle 72 – 144 – 288 was also considered important by Gann. You may have heard or read of “the square of 144.” Gann used the term “square” to refer to a significant market cycle. You will recall that 144 is a Fibonacci number. It is also the natural square of 12, 12 x 12 = 144. Natural squares are also important. The number 72 is half of 144, but also twice 36, which is the natural square of 6. The number 288 is twice 144, but it’s also only 1 away from the natural square of 17, which is 289. Hence what we see is that 144 is probably no more significant than any other natural square, except that it is also a Fibonacci number and closely related to other natural squares around it. Therefore, in my own trading I accord this cycle with some importance.

Gann also considered 52 as a significant trend change cycle. This probably also is based on an astronomical phenomena. Thus far we have seen Gann consider 7, 30, and 52 as important numbers. These are the number of days in a week, days in a month, and weeks in a year. As well, the slope of the Great Pyramid walls was approximately 52 degrees. I have seen this cycle of 52 work in the stock market particularly, but its influence fades in and out. It can be considered of significance in some markets.

Gann often divided trading ranges and other numbers into eighths. Each of these 1/8th divisions then also became important. There is more than one possibility as to why Gann chose to do this. One is the 45 degree and 360 degree relationship. Both 45 and 360 are significant numbers which are recurrent using a variety of geometric and astronomical techniques. Since 45 is exactly 1/8th of 360, Gann may have chosen to carry this relationship forward and apply it to other trading situations.

However, I believe that the real basis for Gann’s division of 8 may well be Fibonacci. The really interesting part of this is that Gann never made reference to Fibonacci in any of his writings. Not even once. This lack of reference is precisely why I believe Gann accorded such great importance to Fibonacci. Let me explain further.

It is well known that Gann was a workaholic, who studied virtually all significant mathematical discoveries, especially those directly involving numbers. Something as mysterious and esoteric as Fibonacci would be something virtually sure to capture the attention of W.D. Gann. While Gann did not specifically mention Fibonacci, I believe Gann understood Fibonacci, and Gann’s Fibonacci short cut was the division of 8ths.

The Fibonacci ratios and the divisions of 8ths are listed side by side below.

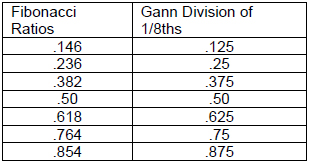
As you can see, the divisions are in fact quite close to each other in absolute terms. Of even greater interest is that the differences are all related by a factor of 7 (382 – 375 = 7, 250 – 236 = 14, 146 – 125 = 21). This also incorporates Gann’s reference to the number 7 as significant.

Again we see that all of the important numbers, cycles, and ratios in price and time are inextricably related and intertwined.